MCHeCalc Routine
| Combining U-Th ion microprobe analysis with (U-Th)/He dating has strong
potential for Quaternary volcano chronostratigraphy. U-Th zircon ages constrain the time
of crystallization, whereas (U-Th)/He dates the eruption. Uranium-series disequilibrium of
long-lived intermediate daughters 230Th and 231Pa, however, requires significant
corrections for Quaternary (U-Th)/He ages. For zircon, deficit in 230Th (~75.7 ka
half-life) causes retarded 4He accumulation compared to secular equilibrium and
consequently (U-Th)/He ages that appear too young. On the other hand, excesses in 231Pa
(~32.8 ka half-life) are expected for zircon, leading to excess He and overestimation of
(U-Th)/He ages. Disequilibrium at the time of crystallization can be corrected through
known partition behavior of parent and daughter isotopes (D parameters), but many volcanic
rocks show evidence for protracted crystal growth and pre-eruptive residence during which
radioactive decay changes initial disequilibrium. For this reason, knowing crystallization
ages through direct measurement of individual crystals is essential.
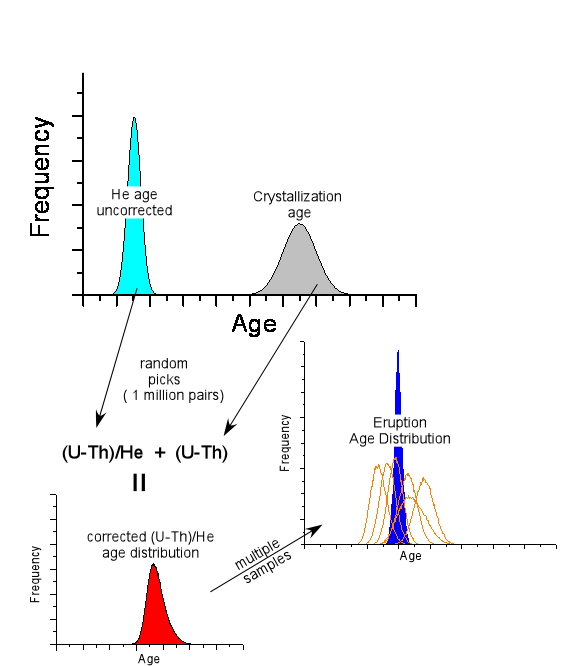
In order to improve disequilibrium corrections for (U-Th)/He dating, we have developed a new computational routine (MCHeCalc) for disequilibrium correction of (U-Th)/He data based on a Monte Carlo simulation. MCHeCalc randomly picks ages from the normal distribution defined by the uncorrected measured (U-Th)/He ages and its uncertainty (light blue Gaussian), and combined it with a randomly pick crystallization age from the normal distribution represented by (U-Th)/He measured age and its uncertainty (blue Gaussian). We calculate the deficit in 230Th and 231Pa (if there is any) at the time of zircon crystallization from the D230 and D231 parameters (D = (Th/U)zircon/(Th/U)melt). Using these parameters and the U-series decay, MCHeCalc calculates a distribution of (U-Th)/He ages corrected by disequilibrium from 1 million trials (pseudo-Gaussian red curve). The software is set to disregard and repeat trials that violate the constraint that eruption must post-date crystallization. |
Download MCHeCalc A "concordant" eruption age probability density function (grey curve) is also calculated from the intersection of all individual zircon corrected age distributions (see right hand panel). This "concordant" age distribution can be represented by its peak age and its asymmetric associated uncertainties. Finally, the program estimates a goodness of fit parameter Q using the incomplete gamma function. |
REFERENCES Eruption Ages of Las Tres Vírgenes Volcano (Baja California): a Tale of Two Helium Isotopes, Quaternary Geochronology. |
|